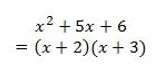Factoring
Review: Expanding Bionomials
To expand binomials you must multiply all terms in the first bracket with the second bracket
-
Once you expand the two brackets it is also important to simplify by collecting like terms
*CONNECTION: Multiplying binomials allows us to get from factored form to standard form.
Example:
Video example:
Common Factoring
Factors are the numbers you multiply together to get another number
When you find the factors of two or more numbers, and then find some factors are the same ("common"), then they are the "common factors".
Example: 12 and 30
• The factors of 12 are: 1, 2, 3, 4, 6 and 12
• The factors of 30 are: 1, 2, 3, 5, 6, 10, 15 and 30
So the common factors of 12 and 30 are: 1, 2, 3 and 6
Website used: https://www.mathsisfun.com/definitions/common-factor.html
Example:
14m + 21n *Common Factor = 7* Steps
7 7 1. Find a common factor between all terms
= 7(2m+3n) 2. Factor it (the common factor) out
3. Place the factored term in front of the bracket. 4. Divide the terms from the original problem with the common factor and place the anwers inside the bracket.
Factoring By Grouping
Often, this type of factoring contains 4 terms
Steps
1. Collect like terms and place the two terms that have a common factor beside each other
2. Factor both sets (each set has two terms)
3. Place the factored term outside the brackets and the remainder inside after dividing the terms by the common factor
4. Repeat step 3 for the second set of two terms
5. Place both terms that are outside of each set of bracket into a new bracket.
6. The terms in the brackets from steps 3 and 4 will be the same so place the terms in brackets beside the new brackets from step 5.
Example:
xy+4x+12++3y
= xy+3y+4x+12
y 4
= y(x+3) + 4(x+3)
= (y+4)(x+3)
Factoring Simple Trinomials
Simple Trinomials have three terms and where the "a" value is 1.
Steps
1. Check and remove all common factors (Must be a common factor in all three terms).
2. Identify the type of trinomial
3. Find the product that would be the product of "c" but the sum of "b" (according to the standard form equation)
4. Optional: Check you answer
Example:
Product of 6: 2x3
Sum of 5: 2+3
Factoring Complex Trinomials
Method: Decomposition
Steps:
1. Multiply the "c" value with the coeffecient f the first term to get the product.
2. The "b" value will be the sum.
3. Find two numbers that would equal to the product (step 1) but the sum of the "b" value (step 2).
4. Factor normally.
Example:
Special Factoring
Perfect Squares
Perfect Squares have three terms
Steps
1. Square root the first and last term
2. Multiply the two new terms by 2.
3. If the product gives you the middle term of the equation then it is a perfect square.
4. Place the two new terms into a set of brackets and place a exponent of two outsde the secong bracket.
Example:
Difference of Squares
Characteristics:
-
Has two terms
-
Second term is a negative number
Steps
1. Square root both terms.
2. Place the new terms into one bracket.
3. For the second set of brackets put the same terms that were in the first one but change the symbol of the second term to the opposite (If it was a negative number it would become a positive and vise versa)
Note: the first term in both brackets should have the same symbol (most likely a positve value)
Example:
CONNECTION:
The following types of factoring start as a standard form equation and become an equation in factored formafter they are factored completely.
-
Common Factoring
-
Factoring by grouping
-
Factoring Simple Trinomials
-
Factoing Complex Trinomials
-
Perfect Squares
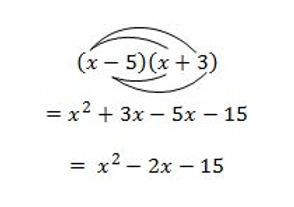
Factored Form equation: y= a(x-r)(x-s)