Vertex Form

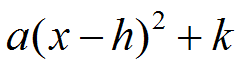
EQUATION:

Affects of each variable on a graph/Transformations

a

If the "a" value id positive the parabola opens up.
if the "a" value is negative the parabola opens down.
Changes the Step Pattern (more information further below)
Vertical Stretch- when the "a" value is a whole number greater than one (Narrow Parabola).
Vertical Compression- when the "a" value is a fraction or decimal less than one (Wide Parabola).

-- If the "a" value is negative the parabola reflects on the x-axis.

-- if "a" is a whole number you write, vertical stretch by a factor of___ (the number)

-- if "a" is a decimal/fraction you write, vertical compression by a factor of __(the number)

h

Determines where the grapgh is located on the x-axis.
The "h" is also known as the axis of symmetry and the x-value of the vertex.
Horizontal shift

- Negative "h" value indicates the parabola is moving right.

- Posittive "h" value indicates the parabola is moving left.

-- If the "h" value negative you write, horizontal shift right ___(value of h) units.

-- If the "h" value is postive you write, horizontal shift left ___(value of h) units.

k

Determines where the graph is located on the y-axis.
The "k" is also known as the optimal value and the y-value of the vertex.
Vertical Shift

- Negative "k" value means the parabola is moving down.

- Positive "k" value indicates the parabola is moving up.

-- If the "k" value is negative you write, vertical shift down___(value of k) units.

-- If the "k" value is postive you write, vertical shift up ___(value of k) units.

Step Pattern

The original step pattern of the basic parabola ( ) is: over 1, up 1, over 2 up 4, over 3 up 9 and etc.
If the "a" value is a number other than 1, you must multiply the "a" value by the original step pattern of 1,4, 9 and etc to find the new y-values of the step pattern **Note: the x-values always remain the same (1,2,3 etc.)
A negative y-value indicates you will move down and a positive y-value indicates you will move up.
It is very important to complete the step pattern on both the right and left side of the vertex.

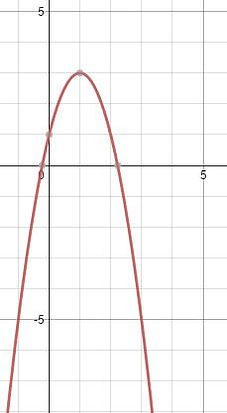
Example

Since the "a" value is negative we know that the parabola will be facing downwards.

Steps

Multiply the "a" value with 1,4,9

- In this case (-2)

1 x (-2)= -2

4 x (-2)= -8

9 x (-2)= -18

2. Determine the vertex

(1,3)

3. Plot the vertex and the new step pattern

- Therfore the new step pattern would be over 1, down 2, over 2 down 8 and over 3 down 18.

The final graph will look like this:

Finding the roots and y-intercept from vertex form

Steps to find the y-intercept

1. Plug "x" as 0.

2. Slove

To find the x-intercepts look at the following exaample.

Example:

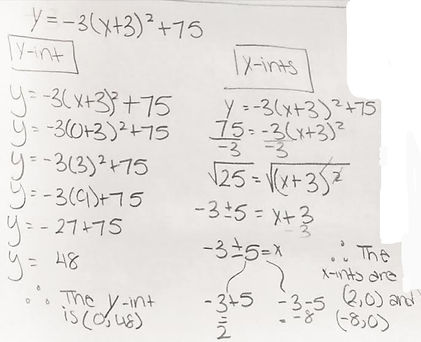
Connection: After finding the roots and y-intercept you can plot the x-intercepts and the vertex which can be determined by the equation.

Vetex Form to Facotred Form then Standard Form

Connection:

After expanding and simplifying, you can find the x-value of the vertex. You can do this by plugging in the values in the equation -b divided by 2a. Then, you can find the y-value of the vertex by plugging in the x-value into the original equation and solving.Another way to get the vertex is look at the vertex form eqaution given. In order to find the zeros, you expland your vertex form equation (so you are know in factored form). Then, set the (x)s to zero and solve for x by isolating it. Now you are able to graph another way.